中学生の皆さんはまだ「微分」というものを習っていないでしょう。でも言葉だけは聞いたことがありませんか。高校に入ればどうせ知ることになるでしょうから、ここで簡単に説明をしておきます。

◎　微分はグラフの傾き

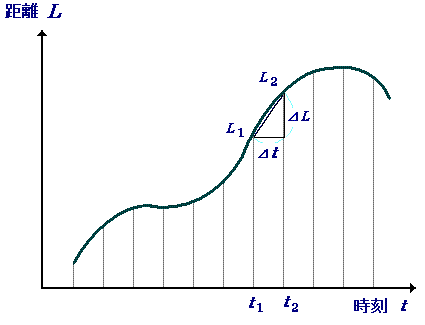
　たとえば下図のように、等速運動でも等加速度運動でもない、勝手な運動をしている物体があったとします。横軸が時刻 で、縦軸は進んだ距離 です。

まあ、あなたのお父さんが自宅への帰り道を、酔っぱらったままフラフラよたよたと歩いている姿を想像してください。 　一般に「速さ」というのは「進んだ距離」を「かかった時間」で割れば算出できますが、このお父さんは、時には止まりかけたり、少し逆戻りしたりしながらも、ランダムな速さで自宅へ向かって進んでいるんです。その瞬間によって速さがいろいろと違うわけですね。

　そこで時間を細かい区間に分けます(たとえば１秒ごと)。そしてその瞬間ごとの速度をみてみようというのです。
　帰り道のある時刻 から、ほんのちょっと時間が経った までの微少な時間 ⊿(秒)に、このお父さんは Ｌ から Ｌ までの ⊿Ｌ(ｍ)の距離を進みました。この区間での速さは、

　　　⊿＝＝　　　　　　　　（ ⊿ は「デルタ」と読みます。）

になりますね。グラフで見てみるとこれはこの間の三角形の傾き、つまりは微少時間での平均の速さに相当します。
　この ⊿ の間隔を狭く取れば取るほど(たとえば 0.1秒ごとにする)、より正確な「瞬間の速さ」を表すことができます。

　もしグラフ全体の ⊿の変化をひとつの式で表せるなら（このお父さんは複雑でランダムな運動なので、ものすごくややこしいな式になるでしょうが）その式は という記号で表現します。これが「微分」の式です。

◎　四次元時空での微分

　お父さんのヨタヨタ歩きだって、東西の方向(方向)だけでなく、南北方向(方向)にずれる場合もあるでしょう。一般に三次元空間を勝手な曲線を描きながら運動する物体(たとえば紙飛行機など)の速度微分については、

　　　 ＝ ，　　 ＝ ，　　 ＝

の３式で立体的に速度変化を式に表すことになります。

　ところが四次元時空において、たとえば光速に近い速さで飛行する宇宙船と地球との間では、そもそも時間の経過そのものが異なるわけですから大問題です。この「時間微分」という考え方では両方の世界をつなぐ式にはなりません。

そこでアインシュタインは運動のグラフ上を、微少な時間に区分するのではなく、運動曲線の弧の長さ Ｓ を微少に分けて (たとえば曲線上を１ｍ動くごとに) 区切って考えたのです。 　式の上では 　 　＝ ，　 ＝ ，　 ＝

となります。これも ⊿Ｓ を狭く取れば取るほど、その瞬間瞬間のお父さんの動きを正確にあらわすことになるでしょう。　

参考文献　　「基礎物理学」 　金原寿郎　裳華房
　　　　　　　　　　　　　　　　　　　「物理学への数学的序説」　荒木源太郎　みすず書房